Don Tow's Website

The impact of quantum physics (also known as quantum mechanics or quantum theory) since its introduction almost 100 years ago has had large and deep impacts on almost all aspects of our lives, including business lives, personal lives, and war and peace between nations. Our everyday usage of electronic appliances, fluorescent light bulbs, televisions, computers, digital cameras, cell phones, Internet, GPS, lasers, electronic microscopes, MRI scans, modern military aircrafts, nuclear submarines, nuclear weapons, etc. all make use of quantum physics.

Quantum physics differs significantly from classical physics. Classical physics describe the physical laws governing the behavior of ordinary size objects that we deal with everyday in our lives – objects like a baseball, a bullet, a musical instrument like a violin, water waves on a beach or in an ocean. Quantum physics describe the physical laws governing the behavior of very small objects that we have to deal with in the subatomic world – objects like an electron, a proton, a neutron, a photon (the constituents of light). This article discusses some of the largest differences between quantum physics and classical physics, and the associated wonders and mysteries of quantum physics.

In classical physics, the objects that we deal with behave either like particles (e.g., a baseball, a coin) or like waves (e.g., a water wave, an air or light wave). Furthermore, an object is either a particle or a wave. But in quantum physics, the objects that we deal with have characteristics of a particle and characteristics of a wave. In other words, the subatomic objects behave both like a particle and a wave. This new and surprising discovery occurred through a series of experiments known as the double-slit experiments from the 19th century to the first quarter of the 20th century. [1]

Series of Crucial Experiments

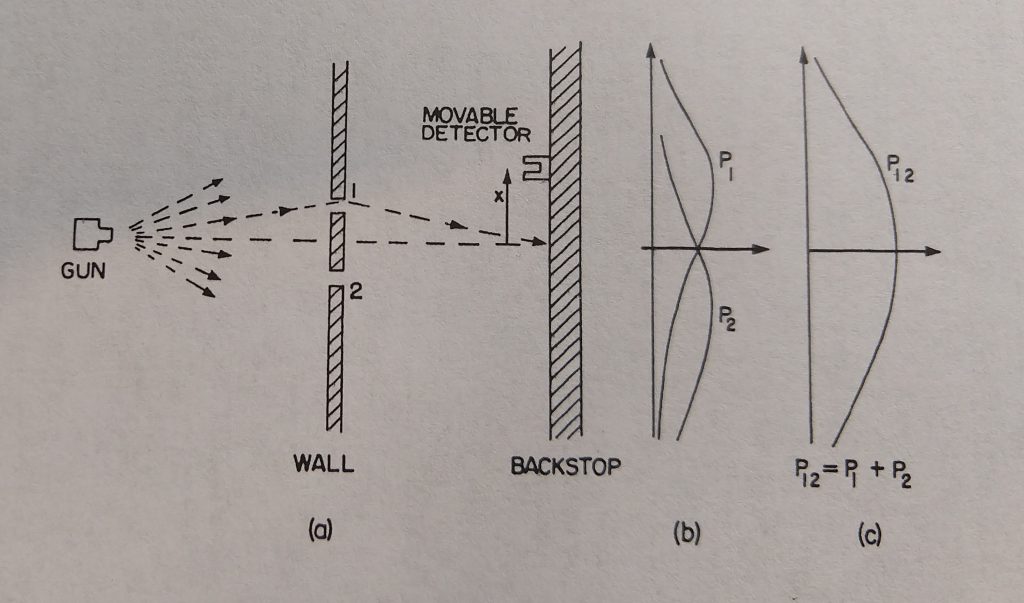
First we discuss the double-slit experiment using a classical object like a bullet from a gun. In this double-slit experiment, there is a source producing the objects of concern, the bullets. Then there is a wall with two slits allowing the bullets to go through. With the exception of the two slits, the wall blocks the bullets. Finally, beyond the wall there are movable detectors mounted on the backstop, with the position of the detectors being movable. This experiment is shown in Figure 1: Double-slit experiment with bullets.

• 

Figure 1: Double Slit Experiment 1 – With Bullets

(from The Feynman Lectures on Physics, Volume 3 – Quantum Mechanics, p. 1-2, Addison-Wesley Publishing Company, 1965)

The movable detector measures the probability of the bullet arriving at the location of the detector. The most likely position of the arriving bullet is the straight line from the gun source through the slit to the backstop. As a matter of fact, if you ignore that the slit is larger than the width of the bullet and a bullet could be deflected by the edges of the slit, the distribution function of the bullet at the backstop will be a delta function, i.e., showing 1 (i.e, 100% probability) at the x-position that is a direct straight path from the bullet source through the slit to the backstop, and zero everywhere else. Because the slit width is larger than the width of the bullet and the bullet hitting the edges of the slit could be deflected, the bullet can be deflected upward or downward with a smaller and smaller probability of arrival the farther the detector deviates from the straight line.

When we do the experiment with Slit 2 closed, the bullet can only go through Slit 1, we find that the probability distribution for the bullet arriving at different positions at the backstop is depicted as P₁ in the above diagram. Similarly, if we do the experiment with slit 1 closed, the bullet can only go through Slit 2, we find that the probability distribution for the bullet arriving at different positions at the backstop is depicted as P₂ in the above diagram.

Now when we do this experiment with both slits open, we find that the probability distribution for the bullet arriving at different positions at the backstop is depicted as P₁₂, which turns out to be exactly the sum of P₁ and P₂, i.e., the sum of the probability of the bullet going through Slit 1 and the probability of the bullet going through Slit 2. Saying it mathematically, there is no interference to the motion of the electron when a second slit is opened and allows it another path to reach the backstop. This behavior of objects like bullets is very much different from the behavior of objects like waves, as in water waves, sound waves, or light waves, which we now discuss.

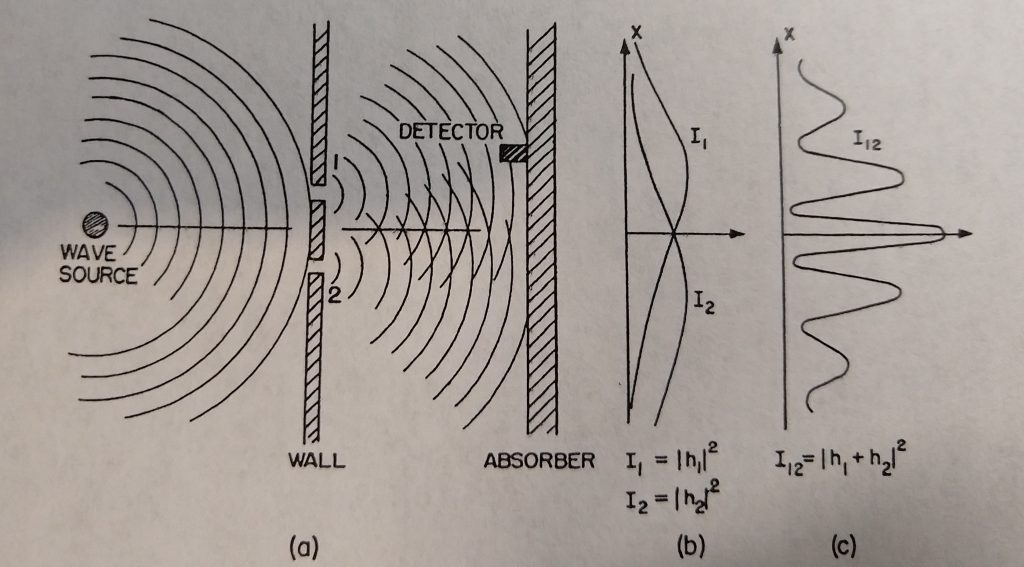
We now perform a similar double slit experiment, but now the source is generating water waves, instead of bullets. and the detector is a gadget that measures the water wave intensity denoted as I, e.g., the height of the wave. This is illustrated in Fig. 2.

• 

Fig. 2: Double Slit Experiment 2 – with Water Waves

(from The Feynman Lectures on Physics, Volume 3 – Quantum Mechanics, p. 1-3, Addison-Wesley Publishing Company, 1965)

Again, when Slit 2 is closed, the measured probability is shown as I₁. Similarly, when Slit 1 is closed, the measured probability is shown as I₂. However, when both slits are opened, the measure probability is shown as I₁₂, which is definitely not the sum of I₁ and I₂. The reason is that with waves, the waves can go through both slits at the same time. Mathematically, the intensity of the water waves for I₁ is the square of a complex function h₁ (complex in the sense of real versus complex numbers), and the intensity of the water waves for I₂ is the square of a complex function h₂. Experimentally, it turns out that the Intensity I₁₂ when both slits are opened is equal to the square of (h₁+h₂), and due to the cross terms, it is not the square of h₁ plus the square of h₂. This means that when both slits are open, there are interference terms (corresponding to the cross terms) because the waves can go through both slits at the same time.

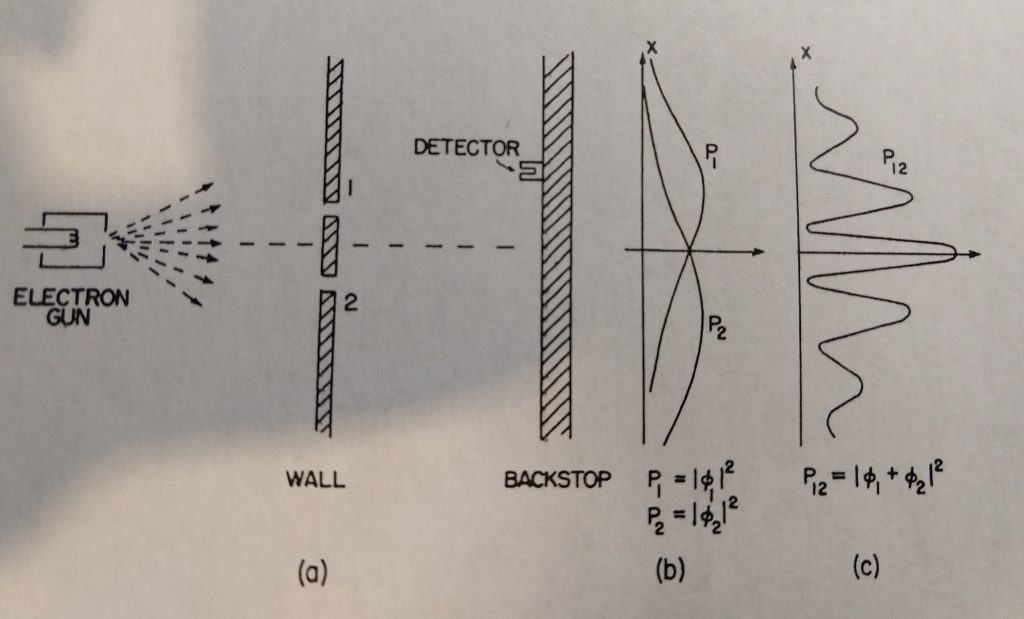
Now, let’s do a third double slit experiment using electrons at the source and counters (such as Geiger counters) at the backstop. The counter in the backstop produces a sound to tell us that the electron has arrived at that location on the backstop.

• 

Fig. 3: Double Slit Experiment 3 – with Electrons

(from The Feynman Lectures on Physics, Volume 3 – Quantum Mechanics, p. 1-4, Addison-Wesley Publishing Company, 1965)

Again, when we block Slit 2, the measured probability distribution at the backstop is shown as P₁. Similarly, when we block Slit 1, the measure probability distribution at the backstop is shown as P₂. However, when both slits are opened, the measured probability distribution surprisingly is shown as P₁₂, which is not the sum of P₁ and P₂. As a matter of fact, if you compare Fig. 3 with Fig. 2 and Fig. 1, the distribution function of the electrons behaves just like the distribution function of water waves, and not like the distribution function of bullets.

Mysteries of Quantum Physics

This series of crucial experiments in the 19th century and first part of the 20th century led to one of the first mysteries found when we deal with very tiny objects like electrons of the subatomic world.

Mystery 1: The behavior of these subatomic objects like electrons behave very differently from macroscopic objects like bullets. Electrons exhibit wave-like properties (similar to what we saw with water waves as in our second experiment).

But this is not the only mystery when dealing in the subatomic world. We now discuss several more mysteries.

Now, if the electrons go through both slits at the same time, when we detect the electrons at the backstop, do we find only part of an electron? From the experiments, we found that the clicks that we hear from the counters in Fig 3 that detect the arrival of the electrons at the backstop are always the same. For example, we don’t hear any half clicks that perhaps indicate that only half of the electron arrived at that location and the other half might have arrived at another location, which may be what you would guess if the electron went through both slits. This means when you detect the electrons, you detect the whole electron, and not only part of the electron, i.e., electrons also behave like particles. This leads to:

Mystery 2: Subatomic objects, although displaying wave-like characteristics, also display particle-like characteristics. This is known as the wave-particle duality of quantum physics., i.e., subatomic particles display both characteristics, showing behavior like a wave, and also showing behavior like a particle.

There are more mysteries of quantum physics. From the previous experiment, we saw that electrons behave with wave-like properties in the sense that they seem to go through both slits at the same time, and they don’t just go through slit 1 or slit 2.

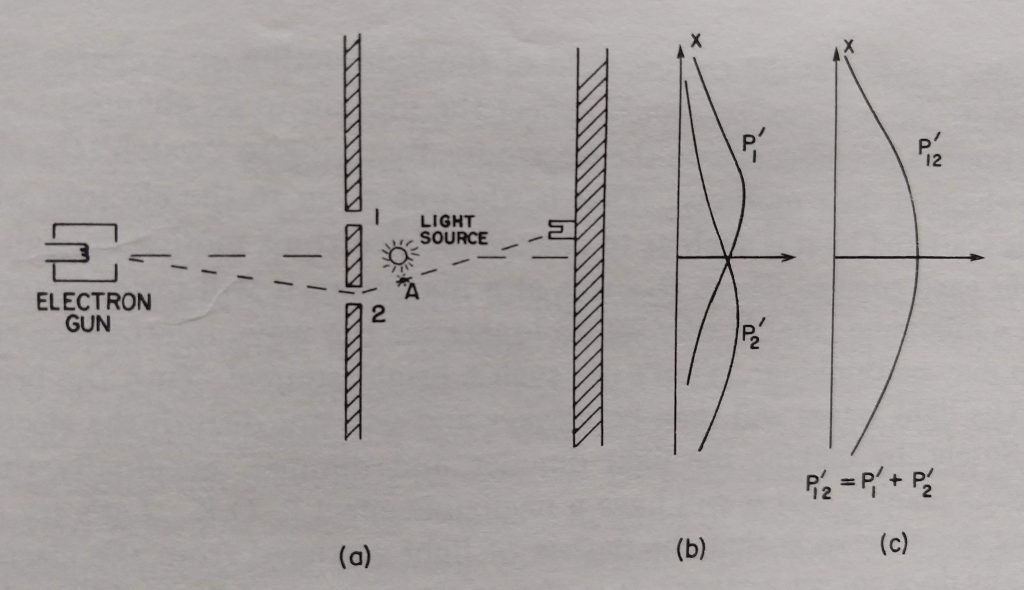
Can we try to detect which slit the electron went through? We know that electric charges scatter light. Since electrons are charged particles, if we put a light source behind the wall, we should be able to determine the path the electron took by observing the location of the scattered light. So let’s do an experiment as depicted in the next figure.

• 

Fig. 4: Enhanced Double Slit Experiment with Electrons and a Detecting Light Source

(from The Feynman Lectures on Physics, Volume 3 – Quantum Mechanics, p. 1-7, Addison-Wesley Publishing Company, 1965)

In this experiment, if the electron went through Slit 2, we should see a flash of light coming from the vicinity of location A in the above diagram. Similarly, if the electron went through Slit 1, we should see a flash of light coming from the vicinity of a location above the light source. If we see flashes of light coming simultaneously from both spots, then we can conclude that the electron went through both slits at the same time.

So when this experiment was done, what did we observe? Whenever we hear a click from the counter at the backstop, we also see a flash of light either near Slit 1 or near Slit 2, but never both. Furthermore, with this experimental setup, the probability distribution observed at the backstop is no longer P₁₂ of Fig. 3, but P₁₂^‘ (i.e., P₁₂Prime) of Fig. 4 (which is similar to P₁₂ of experiment 1), i.e., there is no longer any interference.

What does this mean? When we observe the location of the scattered light to determine the path of the electron, the observing light gave some momentum to the electron and disturbed the path of the electron and changed the original distribution pattern. If you keep on reducing the momentum of the observing light passed on to the electron (by reducing the light frequency or increasing its wavelength), then when you increase the wavelength more and more, you increase more and more the uncertainty on the position of the scattered light. When you reach the point of being unable to detect the location of the electron, the distribution pattern at the backstop also changes back from P₁₂^‘ (i.e., P₁₂Prime) of Fig. 4 to P₁₂ of Fig. 3! This leads to the following:

Mystery 3: The act of observance can change what you are observing. This is understandable for the experiments discussed above because in order to observe, you need to use light. In order to give more precision to what you are observing, you have to use smaller and smaller wavelengths (or larger and larger frequencies of light), which is equivalent to imparting larger and larger momentum to the electrons and therefore results in larger and larger disturbance to the path of the electrons.

This also leads to:

Mystery 4 Heisenberg’s Uncertainty Principle – One cannot simultaneously measure precisely the position and momentum of any object (first proposed in 1927 by the German physicist Werner Heisenberg).

This uncertainty principle applies not just for the position and momentum of any object, it actually applies for any pair of complementary (or conjugate) variables, like time and energy of an object. Furthermore, it is an intrinsic limitation of nature, and not just due to inadequacy of the accuracy of our current experiments.

The uncertainty principle leads to one of the most significant and puzzling implications of quantum physics: Something may be created from “nothing.” We often think of a vacuum as made up of empty space. However, if we are talking about an extremely tiny interval of time, as at the moment of the Big Bang when our current universe was created, then the uncertainty principle tells us that the uncertainty in the involved energy could be very large, large enough to create electron and positron pairs, or mater and anti-matter pairs to form stars and galaxies. This is known as vacuum polarization or vacuum fluctuation. That means that things may be created from the nothingness in a vacuum. [2] However, solving this mystery of creating something from nothing leads to another great mystery that currently we have no clue of solving, i.e., why is there not an equal amount of matter and anti-matter, instead of our observed universe which is made up of essentially only matter.

Predictability of Quantum Physics

In classical physics, if we are given the initial conditions of an object, then using the laws of physics, we can predict precisely the future behavior of an object. However, in the subatomic world, because particles have wave-like characteristics, we can no longer predict precisely the behavior of an object even if given the initial conditions.

Mathematical digression: The physical state is described by a complex wave function (complex in the mathematical sense of real versus complex numbers), which we denote as C (or the Greek letter phi ϕ in Fig. 3). The distribution function is determined as the square of C. In the double slit experiment, when only Slit 1 is open, that function is C₁. When only Slit 2 is open, that function is C₂. When both slits are opened, the distribution function is the square of the sum of C₁ and C₂, which is not the same as the sum of C₁ squared and C₂ squared. When you do this square calculation, there will be cross terms involving both C₁ and C₂. These cross terms are the interference terms coming from the fact that the wave can go through both slits 1 and 2.

Because in quantum theory, the state of an object is described by a wave function, we can calculate only the probability distribution of the future, and unlike classical physics where we can calculate precisely the object’s future state. This leads to another mystery of quantum physics.

Mystery 5: In the subatomic world, we can only predict the probability distribution of certain physical happenings in the future.

As we stated at the beginning of this article, on the one hand quantum physics has introduced many wonders and has revolutionized essentially all aspects of our lives. It has introduced all kinds of gadgets, like vacuum tubes, transistors, TVs, computers, video games, medical imaging, cell phones, GPS, Internet, nuclear weapons, missiles, and so on. However, on the other hand, quantum physics has also led us to many mysteries, like the wave-particle duality and the probability interpretation of quantum physics. That has led many people, including Albert Einstein, to make the remark that God does not play dice and question whether there is a more fundamental theory than quantum theory so that the uncertainties. can be removed and the theory can then be deterministic, and not probabilistic.

Interpretations of Quantum Theory

As just stated, the probabilistic interpretation of quantum theory has led many people to feel that quantum theory cannot be the ultimate theory of physics. For example, perhaps there are some hidden variables that we are not aware of and therefore we have not defined their values. In the future, if we can figure out what these hidden variables are and determine their values, then we can remove the uncertainties and our physical theory then becomes deterministic. This is known as the hidden variable theory.

In 1964, the Irish physicist John Bell proved a very simple theorem that states that all local hidden variable theories [3] cannot make the same predictions as quantum theory. Therefore, one can perform experiments to prove whether quantum theory or local hidden variable theory is correct.

Even though Bell’s Theorem is one of the most important and remarkable theorems in physics, it is relatively simple to prove in terms of the length of the proof and the sophistication of the required mathematics. But the proof requires some ingenious use of mathematics and logic.

In a future article, we will discuss Bell’s Theorem and the experiments that have been done which so far have shown that quantum theory is the correct theory. [4] Also, in another future article, we will discuss the quantum entanglement from the wave function description of quantum theory and its implications for encryption in quantum computers.

---

[1] The discussion that we use in this article follows closely the lectures of Richard P. Feynman, in The Feynman Lectures on Physics, Volume 3, by Feynman, Leighton, and Sands, Addison-Wesley Publishing Company Inc., Palo Alto, 1965. This series of lectures came from the lectures that Feynman gave for the freshman and sophomore physics courses at Cal Tech in 1961-1963. Although they were intended for college freshmen and sophomores, they have been valuable references for many graduate students.

[2] On the subject of Heisenberg’s Uncertainty Principle and creating something from the vacuum via vacuum fluctuations, there is a good and interesting science documentary “Everything and Nothing: What is Nothing? – 2019 (https://www.youtube.com/watch?v=gXbIzc3bcT8). This is part of a series of science documentaries by Professor Jim Al-Khalili.

[3] Bell’s Theorem applies only to hidden variable theories that are local, i.e., no information can be transmitted faster than the speed of light.

[4] Another good and interesting science documentary of Professor Jim Al-Khalili’ series of science documentaries is “The Secret Of Quantum Physics: Einstein’s Nightmare” – 2019 (https://www.youtube.com/watch?v=f_4nYgrDJvc). This discusses the double slit experiments, the mysteries of quantum physics, and Bell’s Theorem.